本文译自Sensors.
“Eventzur G. GNSS/INS Fusion with Virtual Lever-Arm Measurements”
原作者:Borko A and Klein I
编者按:组合导航系统通常用GNSS信息辅助 INS(Inertial Navigation System),消除 INS 累计误差。这篇论文作者提出了一种使用虚拟杆臂辅助INS的新方法,能够提高INS的定位精度。本文提出的方法较为新颖,收录于18年Sensors期刊。
摘要
大多数平台的导航系统都是基于惯导(INS)搭建。INS的误差一般会随时间累积。为了避免这种现象,通常会使用外界其他信息源(如GNSS)辅助INS,从而消除累积误差。本文提出了一种使用虚拟杆臂测量辅助INS的新方法,从而可以提高INS的精度,即使在静止状态,该测量也能够辅助INS。最后,通过仿真和实验验证了这种新方法的有效性。
1. 前言
惯性导航系统(INS)和卫星导航系统(GNSS)组合可以发挥二者的优势,克服二者的不足。过往学者提出了多种二者组合的架构,包括松耦合,紧耦合,超紧耦合等。相比于松耦合,在卫星个数少于4颗的条件下,紧耦合技术也能够通过对INS和GNSS分别输出的伪距和伪距率进行组合,从而估计出INS的偏差。
实际应用中,应用较多的是松耦合技术,因为GNSS接收机能够直接输出载体运动的特征信息,包括位置和速度,尤其在RTK条件下,可以充分利用RTK的高精度位置和速度信息,通过GNSS接收机输出的位置和速度与INS输出的位置和速度组合,也可对INS的偏差进行估计。但是在卫星个数少于4颗的条件下,松耦合技术将无法使用,即卫星失锁,此时只能通过INS进行航迹推算。
在实际使用过程中,INS和GNSS天线通常存在安装位置误差(杆臂误差),天线被安装于车外,而INS被安装于车内,因此需要对这个安装位置误差进行补偿。本文从另外一个角度理解这个误差,假设该杆臂误差能够准确测量,那么如果使用这个准确测量的杆臂值作为测量值对INS进行辅助,丰富了测量信息,可以进一步辅助INS,从而提升性能。
基于这一基本原理,本文建立了基于15状态的标准滤波算法和基于18状态的滤波算法,18状态滤波算法相较于15状态滤波算法而言,多了三个杆臂估计值作为状态。对这两种滤波算法进行对比,我们发现基于18状态的滤波算法的性能要优于15状态的滤波算法。下文将介绍具体算法。
2. 导航方程
这一部分将介绍三部分模型,分别是INS算法,误差模型和测量模型。
2.1 INS积分算法
这里使用局部坐标系标示载体的位置速度和姿态,加速度和角速度偏差在载体坐标系下建模为恒定偏差。
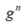
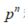 和
和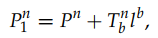 是导航坐标系下的位置和速度测量,
是导航坐标系下的位置和速度测量,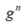 是重力矢量,
是重力矢量, 是载体坐标系至导航坐标系的姿态变换矩阵,
是载体坐标系至导航坐标系的姿态变换矩阵,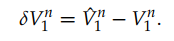 和
和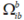 是载体坐标系下的比力和角速度反对称矩阵。下标i和e分别表示惯性坐标系和地心坐标系(ECEF)。
是载体坐标系下的比力和角速度反对称矩阵。下标i和e分别表示惯性坐标系和地心坐标系(ECEF)。2.2 误差模型
为了导出误差模型,定义如下误差状态
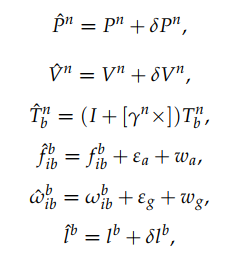
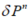 和
和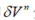 分别是位置和速度误差测量矢量,
分别是位置和速度误差测量矢量,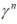 和
和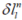 是姿态误差向量和姿态误差的反对称矩阵,
是姿态误差向量和姿态误差的反对称矩阵,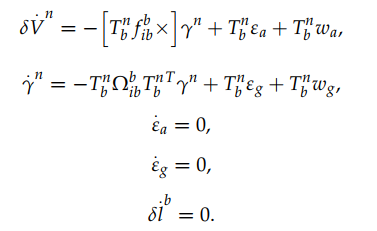 和
和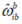 是比力和陀螺测量矢量,
是比力和陀螺测量矢量,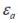 和
和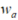 是加速度计零偏和高斯白噪声,
是加速度计零偏和高斯白噪声,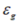 和
和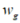 是陀螺零偏和高斯白噪声,
是陀螺零偏和高斯白噪声,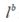 是载体坐标系下的杆臂测量矢量。
是载体坐标系下的杆臂测量矢量。2.2.1 15状态模型
15状态模型中包含位置、速度、姿态、加速度计、角速度计和杆臂值误差,这里省略位置误差。所以线性模型由下面公式给出
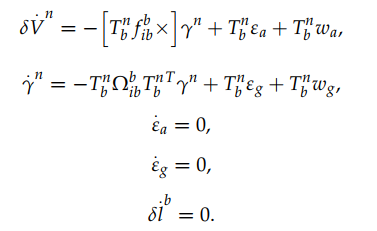
状态变量为
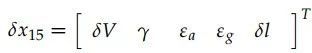
2.2.2 18状态模型
18状态模型相比于15状态模型,增加了位置误差,其他动态方程和15状态相同。额外的位置误差动态为
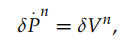
状态变量为

2.3 测量模型
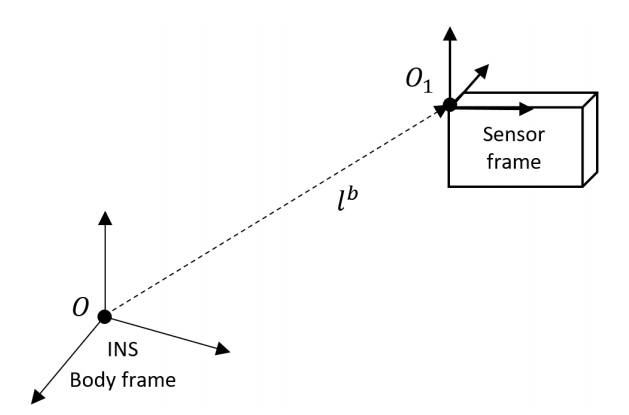
图1INS和GNSS安装示意图
我们考虑上图所示的GNSS和INS。由于GNSS和INS相对距离是固定的,所以这个固定的距离可以作为虚拟测量去辅助INS。测量模型可以写为:
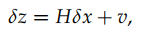
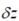 是测量误差向量,H是测量矩阵,v是测量误差。
是测量误差向量,H是测量矩阵,v是测量误差。2.3.1 速度辅助
带杆臂补偿的速度测量由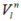 给出:
给出:
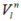 给出:
给出: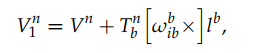
INS和GNSS的测量误差值由 给出:
给出:
 给出:
给出: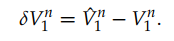
将INS速度和GNSS速度作差可得到 和状态相关的具体表达式:
和状态相关的具体表达式:
 和状态相关的具体表达式:
和状态相关的具体表达式: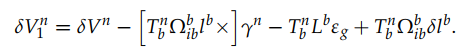
2.3.2 位置辅助
带杆臂补偿的位置测量由 给出:
给出:
 给出:
给出: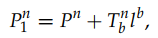
INS和GNSS的测量误差值由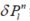 给出:
给出:
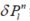 给出:
给出: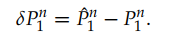
将INS速度和GNSS位置作差可得到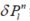 和状态相关的具体表达式:
和状态相关的具体表达式:
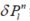 和状态相关的具体表达式:
和状态相关的具体表达式: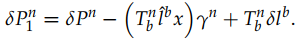
2.3.3 虚拟杆臂测量辅助
对于大多数系统而言,INS和GNSS之间的杆臂值是一个定值,然而由于测量误差和解算误差,INS和GNSS间的距离会改变,所以这个定值可以作为虚拟量测来辅助INS与GNSS,这就是虚拟杆臂辅助INS的基本原理。杆臂值的测量误差由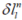 给出。
给出。
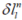 给出。
给出。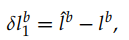
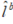 是杆臂估计值,
是杆臂估计值,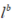 是测量的已知值。
是测量的已知值。3. 实验结果
100Hz的加速度传感器和陀螺传感器的信号从LG-G3手机中获取,1Hz的GNSS信号由Triumph-1型号接收机给出。手机和GNSS天线均安装在车顶,杆臂测量值为[0 1.8 0]。测试工况包含了,40s静止,60s加速和直线行驶,最后两个绕圆行驶。
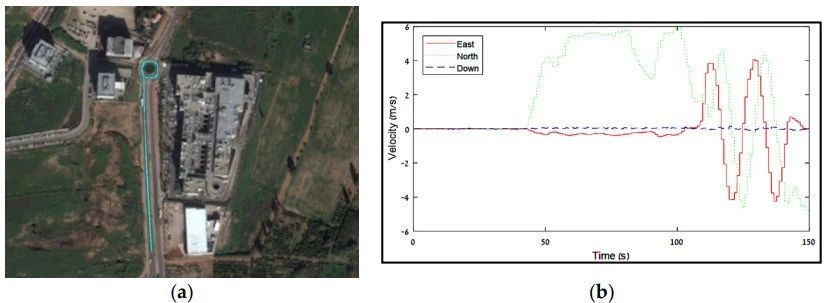
图2 GNSS测得的行驶轨迹(a)和速度曲线(b)

图3 位置估计误差和杆臂估计误差的标准差曲线
图3 给出了位置估计误差和杆臂估计误差的标准差曲线,一种是没有虚拟杆臂测量值辅助的组合导航结果,另外一种是带虚拟杆臂测量值的组合导航结果。没有杆臂测量值辅助的结果中,水平杆臂测量值只有在转向工况下开始收敛,垂直杆臂值一直保持恒定。位置误差在静止时能够稳定在0.8m,当杆臂误差开始收敛时,水平位置误差也开始减小至0.4m。
当有虚拟杆臂测量时,位置误差从一开始就迅速收敛至0.4m,说明这种通过虚拟杆臂测量值的方式可以提高组合算法性能,较好的辅助INS。
4.结论
本文提出了一种通过虚拟测量杆臂值辅助INS的新方法。仿真和实车实验均验证了这种辅助算法的有效性,尤其是在静止和直线行驶工况,该辅助效果更加明显。未来的工作将着重将该算法应用于减小位置估计误差,尤其是在杆臂值难以测量的大尺度平台上面。
联系电话 021-69589225
联系邮箱 11666104@tongji.edu.cn
联系人 李老师
来源:同济智能汽车研究所