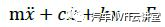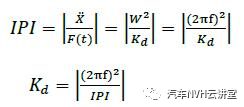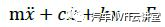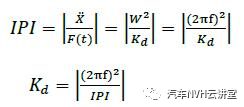基于灵敏度分析的白车身右悬置安装点动刚度优化设计_设计与研发_

论述动刚度与灵敏度分析的理论基础，计算白车身的发动机悬置安装点动刚度，以右悬置安装区域的零件板厚为设计变量，建立发动机右悬置安装点动刚度的灵敏度分析模型，通过OptiStruct优化零件板厚使动刚度计算结果达到设计的目标值。

1 前言

随着汽车工业的快速发展，消费者对轿车舒适性的要求越来越高，轿车的NVH性能在消费者中越来越受重视。白车身关键点动刚度对车身的振动和疲劳破坏有重要的影响，如果该处动刚度不足会导致轿车发动机在一定频率范围内加速产生明显的轰鸣音，严重影响消费者的舒适性体验。振动源头通过车身传递传给乘客，所以通过优化设计传递路径中的车身结构是提高NVH性能的重要方法。本文对某车型白车身悬置安装点动刚度进行计算，发现悬置安装点动刚度不满足目标要求。基于灵敏度分析找出影响发动机悬置安装点动刚度的薄弱区域进行加强，使最终安装点处的动刚度达到目标要求。

2 灵敏度分析与动刚度的理论基础

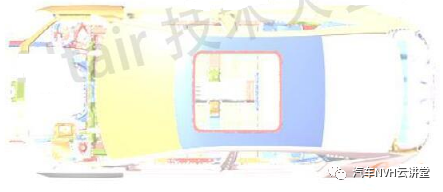
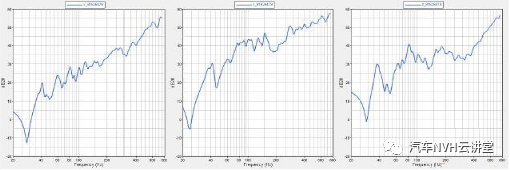
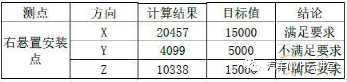
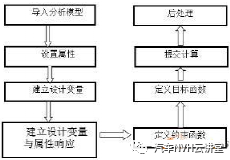
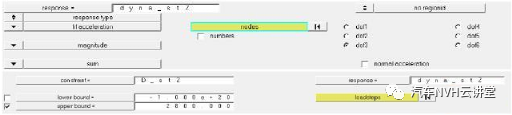
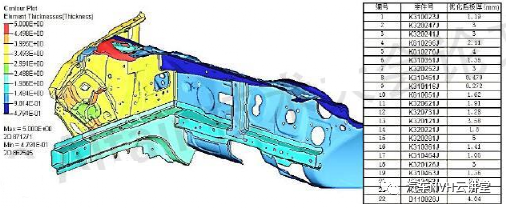
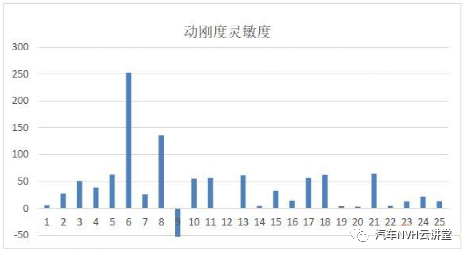
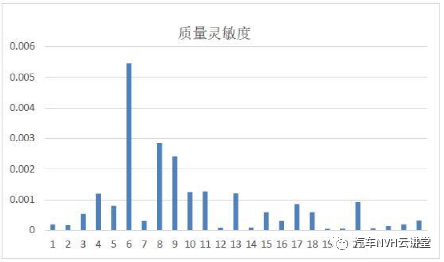
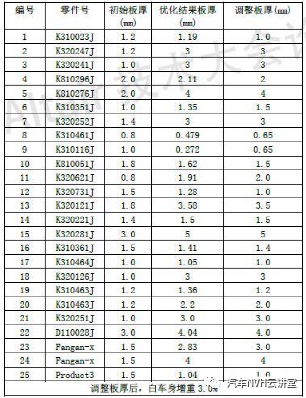
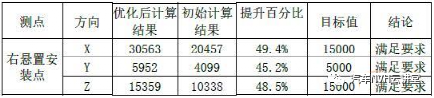
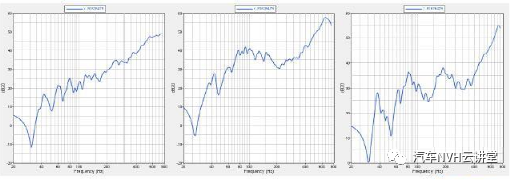
在结构设计目标达成与优化过程中有许多设计参数可供调整，通过灵敏度分析可以快速的识别各个设计参数对设计目标的影响大小，从而避免结构修改中的盲目性，提高设计效率。灵敏度分析对于结构的设计有重要的作用，基于灵敏度分析可以实现汽车结构的轻量化设计，灵敏度是一个广泛的概念，从数学意义上讲，若函数F(X)可导，则一阶灵敏度为：

动刚度的理论计算可用弹簧一阻尼模型进行阐述，其动力学计算公式如下所示：

式中：m为系统质量；c为阻尼；k为静刚度；x为系统位移；F为激励力；w为激振频率；Kd为系统的动刚度。

以上为动刚度的理论计算方法， CAE仿真软件中输出加速度随频率的响应曲线IPI，然后对公式进行如下转换，动刚度的计算参照公式。

本文结合灵敏度分析的理论与动刚度的计算方法，通过仿真软件建立结构动刚度的灵敏度分析模型，找出最优的结构设计方案。

3 白车身悬置安装点动刚度有限元模型

如图1所示为白车身的有限元网格模型，右悬置安装点如图2所示，设计要求右悬置安装点动刚度X向15000N/mm，Y向5000N/mm，Z向15000N/mm。仿真计算时白车身边界条件为无约束自由状态，分别施加X、Y、Z三个方向的激励，右悬置安装点加速度随频率响应如图3所示，根据公式(6)计算动刚度值，计算结果如表1所示，其在Y、Z向的动刚度没有达到目标要求，尤其Z向离目标差距很大。

图1 白车身有限元模型示意图

图2 右悬置安装点结构示意图

图3 右悬置安装点加速度随频率响应曲线

表1 右悬置安装点动刚度(N/mm)计算结果

4 灵敏度分析与优化

由于右悬置安装点Z向离目标要求差距较大，针对Z向动刚度进行灵敏度分析，选取右悬置安装范围的25个零件板厚作为设计变量如图4所示，考虑通过增加最少的质量成本来达成动刚度的目标要求，以右悬置安装点Z向动刚度为约束条件，以白车身的质量最小化作为目标，优化仿真的操作流程如图5所示，根据公式将对动刚度的约束转换为对加速度响应的约束，如图6所示。OptiStruct优化计算结果如图7所示，各个零件板厚对动刚度和质量的灵敏度如图8、9所示，根据灵敏度计算结果，加强或增厚相对动刚度灵敏度高，即质量小且对动刚度敏感的板件，减薄相对动刚度灵敏度低，即质量大且对动刚度不敏感的板件，从而得出最佳优化方案。