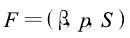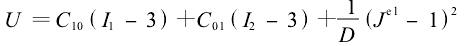空气弹簧因其变刚度、低自振频率、高度可控及良好的高频振动吸收和隔声性能等优点,成为车辆悬架广泛采用的非线性弹性元件和减振元件。空气弹簧囊体是由承载骨架材料(帘线)和橡胶组成的十分复杂的柔性结构(如图1),其断面形状设计理论主要是根据帘线受力与轮廓形状的关系而建立的,由此可见分析帘线力在空气弹簧结构设计中的重要作用。然而目前国内外文献中关于空气弹簧帘线受力特征的研究报道却较为少见。
影响帘线受力的因素很多,如加载条件、气囊断面的形状和尺寸、帘线角、帘线层数等等。由于空气弹簧性能分析过程是包含几何、材料、边界三重强非线性问题,传统理论方法计算比较困难,所以作者用ABAQUS软件对囊体帘线受力的基本特征进行初步研究,该软件在空气弹簧气体压力的定义上有别于其他非线性有限元软件,如MARC非线性有限元软件。其区别在于ABAQUS软件具有符合流体静力学条件的充腔流体单元,该流体单元可以使结构变形和作用在边界上的流体压力之间相互耦合,能够真实地再现空气弹簧在振动过程中腔内气体压力的变化。然而,其他有限元软件在气体压力定义时,只能对空气弹簧腔内壁施加定值压力,该压力在空气弹簧工作过程中是不变的,与实际情况不符。

图1 空气弹簧典型气囊结构
1 空气弹簧有限元建模
作者分析研究的空气弹簧是某型膜式空气弹簧,基本参数如表1所示。
表1 膜式空气弹簧基本参数

1.1 空气弹簧气囊
1.1.1 橡胶材料力学特性
假设橡胶材料为各向异性、不可压缩的超弹性材料,不考虑橡胶的粘弹性。其力学特性可用Mooney-Rivlin模型应变能密度函数描述:

式中:C10,C01和D是与温度有关的材料参数;I1,I2是第一和第二偏应变量,I1=λ21+λ22+λ23,I2=λ-21+λ-22+λ-23,其中λ1,λ2和λ3为三个拉伸方向的拉伸系数;Jel为弹性体积比。
1.1.2 帘线层结构有限元模拟
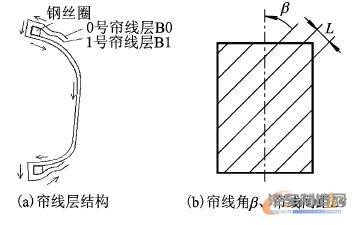
帘线是橡胶气囊的主要承载部件,材料为小变形的尼龙或者聚脂。由于帘线与橡胶基体拉伸模量等物理性能不等,使得帘线层具有复杂的力学各向异性和非线性特征。非线性有限元软件ABAQUS提供了加强筋结构的Rebar单元,能够比较合理地模拟帘线复合材料特性。在空气弹簧帘线层建模中,采用2层反对称结构,帘线力取值路径沿着(图2a)所示箭头方向。按照帘线与垂直方向夹角β(图2b),帘线横截面积,帘线间距L(图2b),帘线层与杂交轴对称单元中性面的偏置以上4个特性建立了帘线层。作者采用线单元模拟Rebar。

1.2 接触
空气弹簧在工作过程中橡胶气囊与活塞和上盖板发生接触,接触问题属于带约束条件的泛函极值问题。ABAQUS中对于变形体与接触体的接触问题采用拉格朗日法。假定橡胶气囊与上盖板和活塞无滑移接触,橡胶气囊为变形体,上盖板和底部活塞为接触体(定义为刚性体)。
1.3 加载
将分析过程分为充气和加载,首先在气囊内壁施加气压,完成后对上盖板施加垂直位移载荷。由于空气弹簧的几何条件、载荷条件和帘线的铺设形式均是轴对称的,因此可以用平面轴对称有限元模型求解,利用轴对称单元来模拟橡胶。
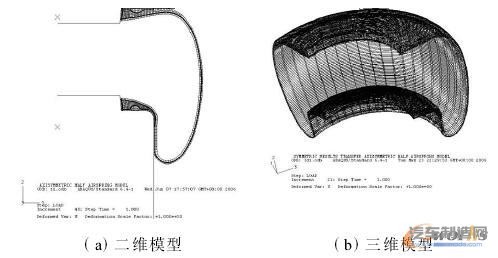
为了提高计算结果的精确度,静载荷下的结构计算必须用三维模型。根据表1参数首先建立空气弹簧纵向截面二维有限元模型如图3a所示,采用Hypermesh软件优化处理截面网格,利用上述单元按照不同材料层离散该截面。然后旋转生成三维模型如图3b所示。

图3 有限元模型
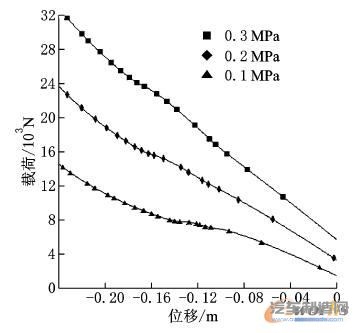
2 空气弹簧的刚度变化特征
此空气弹簧在不同初始气压下的刚度曲线如图4所示,具有空气弹簧非线性弹性特征。随着初始气压的增大,空气弹簧刚度增大。从图中可以看出,此气囊适应载荷范围较大。

3 囊体帘线受力的计算结果和分析
空气弹簧各部分帘线受力可表示为

其中:F表示单根帘线所受轴向力;β表示帘线角;p表示气囊内压;S表示垂直下沉量。分别改变这三个参数,详细地分析空气弹簧囊体帘线受力的变化规律。
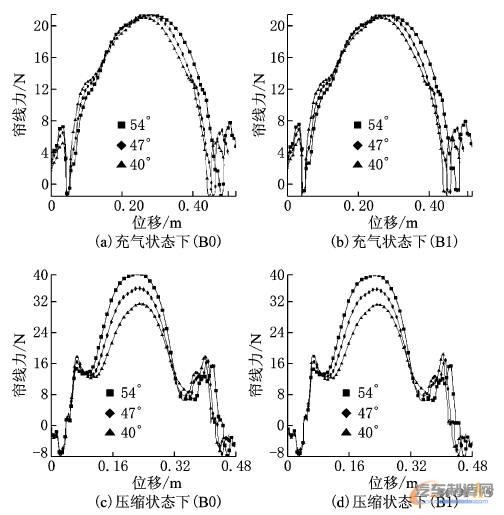
(1)β= 40°,47°,54°;p=0.3MPa;S=0.23m(方向向下)条件下建立的3个模型进行计算,得出B0,B1帘线力分别在充气和压缩状态下的变化特征如图5所示。
比较分析:
①充气状态,3个模型的B0,B1层帘线受力总体趋势呈对称布置,在气囊体中部达到最大值。随着帘线角的增大,在气囊相同部位的帘线力增加。B0,B1的帘线受力情况基本相同,数值变化不大,分布形态相似。
②压缩状态,B0,B1在气囊中部达到最大值。随着帘线角的增大,在气囊相同部位的帘线力增加,增幅可达8N左右。由于气囊与上盖板和底部活塞相接触,在沿帘线力取值路径约0.06m和0.40m处产生局部弯曲变形,使得此部分帘线力数值产生波动,如图5c,5d所示。
③比较B0,B1在充气和压缩状态帘线力可以发现,帘线角的改变对充气状态下的帘线力影响不大,但是却对压缩状态下的帘线受力发生较大影响,因此可以通过调节帘线角改变气囊中部帘线在承担压缩受载时的作用。

图5 帘线角改变条件下帘线力分布图
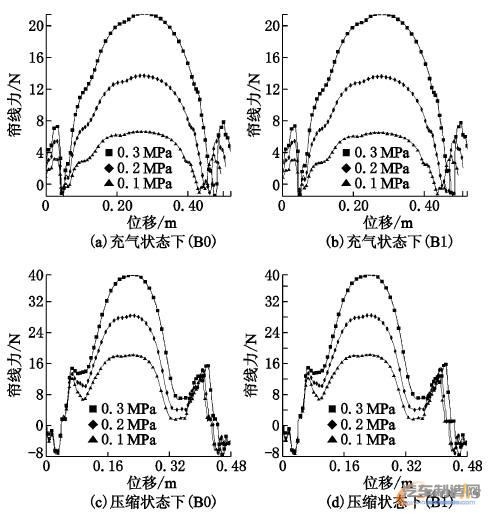
(2)β= 54°,p=0.1,0.2,0.3MPa,S=0.23m(方向向下)条件下建立3个模型进行计算,得出B0,B1帘线力分别在充气和压缩状态下的变化特征,如图6所示。

图6 初始气压条件改变下帘线力分布图
比较分析:
①充气状态,3个模型的B0,B1层帘线受力总体趋势呈对称布置,在气囊体中部达到最大值。随着初始气压的增大,B0,B1在气囊相同部位的帘线力增加,且数值增加较大,增幅可达16N左右。
②压缩状态,B0,B1在气囊中部达到最大值。随着初始气压的增大,在气囊相同部位的帘线力增加,数值变化较大,增幅可达20N左右。同样由于气囊与上盖板和底部活塞相接触,在沿帘线力取值路径0.06m和0.40m左右处产生较大局部弯曲变形,使得此部分帘线力数值产生波动,如图6c,6d所示。
③比较B0,B1在充气和压缩状态帘线力可以发现,初始气压的改变对充气状态和压缩状态下的帘线受力发生较大影响,因此可以通过调节初始气压,明显地改变气囊中部帘线在承担充气或压缩过程中受载时的作用。
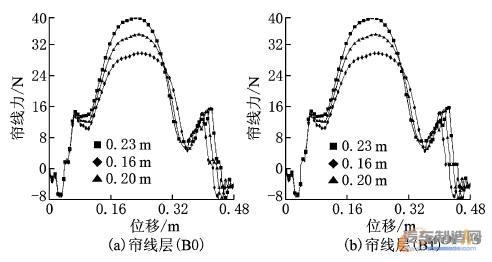
(3)β= 54°,p=0.3MPa,S=0.23,0.20,0.16m(方向向下)条件下建立3个模型进行计算,得出B0,B1帘线力在压缩状态下的变化特征如图7所示。

图7 下沉量改变条件下帘线力分布图
1)充气状态时帘线力分布情况:由于改变的是下沉量,不影响充气状态的帘线力,因此参考图5a中54°充气状态曲线。
2)比较分析:①压缩状态,在气囊中部达到最大值。随着下沉量的增加,气囊相同部位帘线力增加,且数值增加较大,增幅可达8N左右。由于气囊与上盖板和底部活塞相接触,在沿帘线力取值路径约0.06m和0.40m处产生较大局部弯曲变形,使得此部分帘线力数值产生波动如图7所示。
②比较B0,B1压缩状态帘线受力可以发现,下沉量的改变对压缩状态下帘线受力发生较大影响。因此可以通过调节下沉量改变气囊中部帘线受力情况,满足工作条件要求。
4 结论
计算结果表明:
(1)气囊在充气状态时,其帘线受力情况基本取决于初始气压,初始气压越大,气囊相同部位帘线受力越大;帘线角对帘线受力有一定影响,但影响幅值不大,帘线角越大,气囊相同部位帘线受力越大。
(2)气囊在压缩状态时,其帘线力随初始气压、帘线角、下沉量的增大而增大,且影响幅值较大。可以通过对影响条件的合理调配,调整气囊帘线在承担压力中的作用。
(3)帘线包裹钢丝圈部分出现受压或张力不足情况,但帘线角、初始气压、下沉量的变化对此部分帘线力影响不大。
(4)从有限元分析角度来看,气囊在充气中可以利用平面轴对称模型。但在压缩过程中气囊与上盖板和底部活塞发生接触,对囊体帘线受力有显著影响且关系复杂。因此必须采用三维模型,但是网格数量大幅度增加,使得求解效率降低。由于B0,B1中部分帘线力出现负值的不利情况,需要进一步对钢丝圈周边结构进行分析,研究此部分帘线受压问题。