曲轴键槽对称度问题的现场测量

在生产现场中，为了提高测量效率和降低测量成本，需要尽可能多地在现场使用较简单的量具测量工件尺寸，即尽可能少去测量室使用三坐标等大型测量设备。曲轴键槽中心平面相对基准平面的对称度是一个现场测量不容易直接实现的项目，本文对此问题进行了探讨，并通过理论分析提出了一种较为简单易行的现场测量方法。

键槽相对基准平面的对称度

1. 对称度要求的提出

我公司生产的直列四缸发动机曲轴，为保证与键配合的零件能够顺利地安装，且安装后的相位角度正确，需要保证曲轴上的键槽相对基准平面(在本文中为曲轴第1、5主轴颈和第1连杆轴颈中心线所形成的平面，见图1中的红色平面)有一个正确的位置，因此提出了键槽中心平面相对基准平面的对称度要求，即键槽的中心平面必须位于距离为公差值T且相对于基准平面对称配置的两平行平面之间的区域。

2. 测量方法

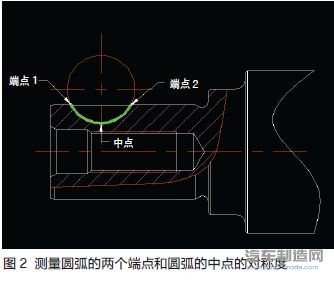
现场测量时，受测量条件的限制，一般都忽略了键槽中心平面的直线度误差和平面度误差，因此现场测量时只需要测量出键槽中心平面轮廓上几个极限点的对称度，其中值最大者即可作为键槽中心平面相对基准平面的对称度。由于键槽为半圆键槽，所以只需要测量出圆弧的两个端点和圆弧中点(见图2)的对称度即可。

直接测量键槽中心平面相对基准平面的对称度存在一定的困难，主要表现为：受键槽宽度较小的限制，测量时不能用普通百分表而只能用杠杆百分表。在测量键槽圆弧中点的对称度时，因为键槽宽度空间较小，所以目视表针圆头部非常不便，在表针前进时操作者难以准确判断表针圆头部是否已经到达键槽底部，通常操作者要等到表针圆头部撞击到键槽底部时才能判断出表针已经到达键槽底部，但这时经常已经造成百分表的读数发生变化。此时，如果操作者没有发现百分表读数变化则会造成测量值错误，如果操作者发现百分表读数变化则不得不重新测量。因此，直接测量影响了测量的准确性和效率。

对称度的理论分析

为了便于后面的说明，我们先定义一个点和二个平面，一个点即“键槽中心点”，在本文中为键槽与轴颈表面相交面的几何中心，如图1中三个平面的交点;一个平面是过键槽中心点且与轴颈中心线垂直的平面，本文称之为“铅垂面”，如图1中的黄色平面;另一个平面是过键槽中心点且与轴颈中心线平行与基准平面垂直的平面，本文称之为“水平面”，如图1中的蓝色平面。

忽略键槽中心平面的平面度误差，则键槽的中心平面为一理想平面，该平面上有这样两条直线，一条直线是键槽中心平面和铅垂面的交线，本文称之为“径向中心线”;另一条是键槽中心平面和水平面的交线，本文称之为“轴向中心线”。两条直线为相交直线，共有3个端点(该3个端点与图2所示的3个点一致)。这3个端点的对称度最大值即为键槽中心平面的对称度。

为方便后面的表达和计算，我们先按图3所示做一些准备工作，其中A点为键槽径向中心线顶端，C点为键槽径向中心线底端，以该两点为顶点如图做直角三角形，三角形的另一个顶点为点B，A点到基准平面的距离为X，C点到基准平面的距离为Y，B点到C点的距离为Z;直线MN为轴向中心线在铅垂面上的投影。

键槽中心线与基准平面的位置关系可归纳为六种，如图3所示，对称度计算方法分为三种：

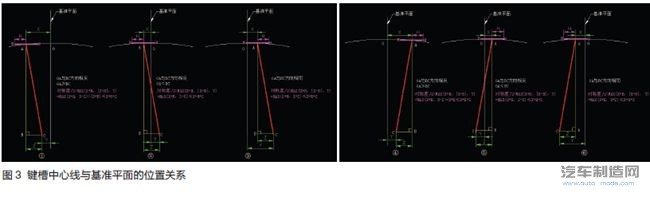
1.在第①和④种情况时，OA与BC方向相反，OA≥BC;键槽中心平面对基准平面的对称度为2×MAX(X+H，|X-H|，Y)=2×(X+H)。

2.在第②和⑤种情况时，OA与BC方向相反，OA

3.在第③和⑥种情况时，OA与BC方向相同;键槽中心线对基准平面的对称度为2×MAX(X+H，|X-H|，Y)=2×[MAX(X+H，X+Z)]。

基本测量方法

根据键槽的使用条件分析，键槽的对称度对装配无直接意义，在其上装配半圆键后半圆键体现出来的对称度才对装配有直接意义。为此，测量时可以模拟半圆键与键槽的配合，设计一种量块(见图4)。为保证其与键槽配合良好，可以按键槽宽度尺寸，每隔0.01 mm为一档，设计不同宽度尺寸的量块。量块的径向长度宜为键槽深度的两倍多一点，量块的轴向长度宜为键槽长度的一倍多一点，以保证将量块塞入键槽后，量规露出部分的尺寸不小于键槽的尺寸(包括径向的深度尺寸和轴向的长度尺寸)。如果量块的尺寸小于键槽的尺寸，测量数值需要乘以一个系数，系数值等于键槽尺寸除以量块尺寸。

该测量方法的具体步骤如下：

1. 先将配合合适的量块塞入键槽，然后将工件找正(为提高测量效率，可以设计专用测具，使工件在测具上放好后理论上即已找正，如图5所示)。

2. 用百分表先测量量块上与键槽中心点对应处(见图5中红线和蓝线交点处)的读数，之后将工件翻转180°，再测量量块上与键槽中心点对应处的读数，两读数做差值再除以2得到的数值即为键槽中心点到基准平面的距离，该值近似等于X。

3. 将百分表沿径向由量块的键槽中心点对应处缓慢移动到量块的远端(见图5中的蓝线)，得到一个差值，该值理论上等

于Z。

4. 将百分表自键槽中心点处沿轴向由量块的一端缓慢移动到量块的另一端(见图5中红线)，得到一个差值，该值理论上等于2H。

5. 根据“理论分析”中介绍的方法计算对称度，判断零件是否合格。

上述测量方法中测量步骤1～4比较容易操作，操作者在进行步骤5时需根据“理论分析”中的方法计算对称度。判断零件是否合格的具体步骤是：首先，判断OA与BC的方向是相反还是相同，如果相同，则再判断H和Z的大小，以确定对称度是2×(X+H)还是2×(X+Z);如果相反，则再判断OA与BC的大小关系;如果OA≥BC，则对称度为2×(X+H);如果OA小于BC，则再判断X+H和Z-X的大小，以确定对称度是2×(X+H)还是2×(Z-X);最后，比较对称度与T(公差值)的大小以判断零件是否合格。

综上所述，该方法中的“步骤5”不仅计算烦索，而且需要操作者进行判断，因此很容易出现错误，存在一定的质量隐患，不符合“防呆防错”思想，因此有必要对其进行简化。

简化测量方法

简化的中心思想是“统一公式，去除判断”，即不需操作者再进行判断，不做或做少量简单的运算，由于“理论分析”中提到的判断公式“X+H”、“X+Z”和“Z-X”均不大于“X+H+Z”，所以如果将判断公式统一成“X+H+Z”，则无论是哪种情况，只会出现把合格品判断成不合格品，而不会出现把不合格品判断成合格品，从而避免了质量隐患。这样简化后，“步骤5”的计算步骤如下：计算(X+Z+H)的值;比较2×(X+Z+H)与T(公差值)的大小，判断零件是否

合格。

由于这样有将合格品判断成不合格品的可能存在，因此当出现“超差品”时，需要操作者或工程师进行再次判别。

虽然该方法已经较简单，但是还是需要进行一次计算。基于此种情况，我们对判断公式再次进行了简化，即对“2×(X+Z+H)≤T(公差值)”进行分解，相当于把对称度指标分解成3个指标，分别是键槽中心点的对称度、径向中心线的倾斜度和轴向中心线的倾斜度。根据现场保证能力，可以均匀分解，即分解成“X≤T(公差值)/6、Z≤T(公差值)/6和H≤T(公差值)/6”;也可不均匀分解，如分解为“X≤T(公差值)/4、Z≤T(公差值)/8和H≤T(公差值)/8”，这样分解后“步骤5”的计算步骤简化为：比较X、Z和H与各自公差值的大小以判断零件是否

合格。

由于操作者的个人习惯和能力存在差异，为了适应不同的操作者，在现场，“2×(X+Z+H)≤T(公差值)”和“X≤T/?、Z≤T/?、H≤T/?”这两种判断方法都是允许使用的。

结语

由于键槽中心平面相对基准平面的对称度在现场难以直接测量，而使用量块间接测量时，其测量结果又非常不直观，甚至可以说理解上存在一定的难度。因此，在我公司，关于键槽中心平面相对基准平面的对称度如何测量以及如何判断还存在着些许分歧。本文就该问题进行了深入探讨，从理论上系统分析了键槽中心平面相对基准平面的对称度的测量方法和计算方法，并根据现场的实际情况，提出了两种较简单易行的测量和判别方法。