CFRP优化汽车顶盖铺层,实现汽车轻量化!
2019-02-01 10:52:30· 来源:湖南大学,汽车车身先进设计制造国家重点实验室 作者:肖志,杜庆勇,莫富灏等
为减少汽车的能源消耗和对环境的污染,轻量化技术得到了广泛关注。复合材料,尤其是连续碳纤维增强复合材料(carbonfiberreinforcedpolymer,CFRP)的应用是实现汽车轻量化的重要途径。CFRP是一种可设计性较强的复合材料,其铺层方式得到
为减少汽车的能源消耗和对环境的污染,轻量化技术得到了广泛关注。复合材料,尤其是连续碳纤维增强复合材料(carbonfiberreinforcedpolymer,CFRP)的应用是实现汽车轻量化的重要途径。CFRP是一种可设计性较强的复合材料,其铺层方式得到了国内外学者的广泛研究。
本文中基于汽车CFRP顶盖制造工艺可行性与抗雪压性能需求,采用自由尺寸优化、尺寸优化和层间组合优化相结合的多层次优化方法对汽车CFRP顶盖进行了铺层设计,以兼顾制件工艺要求与性能目标。
CFRP力学性能测定
1、CFRP样件制备
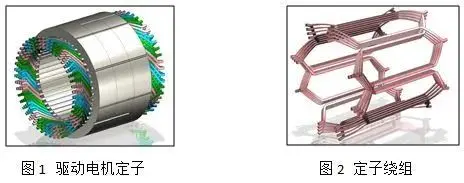
在数值分析过程中,材料本构参数的正确获取与分析结果的准确性有着密切的关系,本文中为获取材料数值模型本构参数,采用试验与数值分析相结合的方法,对CFRP开展相关研究。在CFRP板材制备试验中,碳纤维选用常州市宏发纵横新材料科技股份有限公司生产的CC-P400-12,树脂选用惠柏新材料科技(上海)股份有限公司生产的环氧树脂LTC-6010A/B。在材料制备过程中,依次在真空辅助成型工艺平台上铺放下脱模布、碳纤维材料、上脱模布、导流网和真空袋等,当密封性和压力达到要求的条件时注入树脂,并在适宜的条件下进行固化处理,从而制备试验用CFRP板材,如图1所示。材料制备平台温度为35℃,预固化时间为4h,后固化温度为80℃,后固化时间为4h。

2、 力学性能试验与参数反求
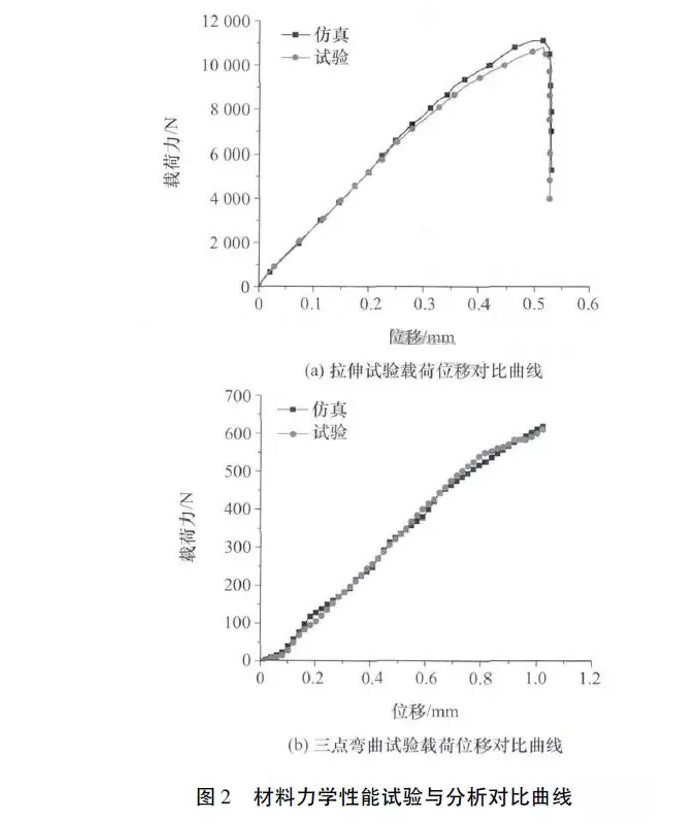
在制备试样板材基础上,为正确获取CFRP数值模型本构参数,开展了材料单向拉伸试验和三点弯曲力学性能试验,并根据试验结果反求材料本构参数,从而保证数值分析模型参数的准确性。CFRP单向拉伸试验和三点弯曲试验分别在微机控制电子万能试验机CMT5105和CMT4304上进行。其中,单向拉伸试验参照标准GB/T3354—1999进行,拉伸速率为2mm/min,环境温度为23℃,样件选用标距(测量长度)为50mm、厚度为1.96mm的8层CFRP试样。三点弯曲试验参照标准GB/T1449—2005进行,加载速率为2mm/min,环境温度为23℃,样件选用跨距为26mm、厚度为2.01mm的8层CFRP试样,试验结果如图2所示。
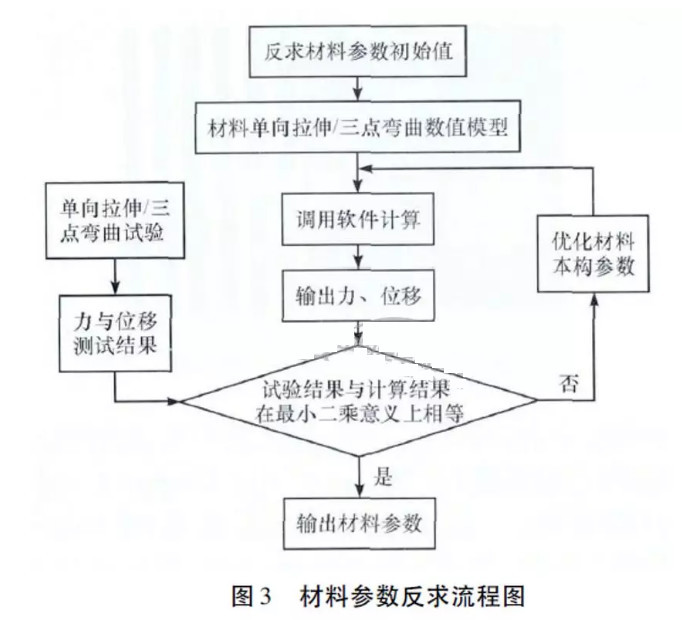
由于材料试验只能获得试件的宏观应力应变曲线等数据,而无法获得试件全场的应力应变分布和损伤演化的具体过程。本文中基于有限单元法建立了CFRP力学性能数值分析模型,在力学性能试验基础上通过材料数值模拟反求材料本构参数,其流程如图3所示。
在CFRP数值分析过程中,通过定义壳单元沿厚度方向的积分点数量来定义复合材料铺层数量,一个积分点代表一个复合材料铺层,每个积分点处的材料坐标系旋转角度代表单层碳纤维的铺层方向角。CFRP失效模拟方式为Chang-Chang失效准则,该准则包含了4种失效准则,即纤维拉伸破坏、纤维压缩破坏、基体开裂和基体挤压,该失效准则的具体表达式如下。
对于纤维拉伸模式σ11>0,则E1=E2=E12=μ12=μ21=0且判断

式中:E1,E2,E12分别为纵向弹性模量、横向弹性模量、面内剪切模量;β为剪切应力比例系数,可人为地定义在纤维拉伸模式下剪切所占的权重,当β=1时,计算失效准则相当于Hashin失效准则,当β=0时,式(1)将等效为最大应力准则,通常情况下,β无法通过试验来获取,需要经过试错法进行标定;μ12,μ21分别为主泊松比及次泊松比;Ftu1,Ftu2,Fcu1,Fcu2,Fsu12分别为纵向拉伸强度、横向拉伸强度、纵向压缩强度、横向压缩强度、面内剪切强度;σ11,σ22和σ12分别为材料在轴向方向、横向方向和面内方向承受的应力;ef,ec,em,ed分别为各模式下判断失效与否的参数。采用LS-DYNA软件对CFRP力学性能进行数值分析,并经试验验证,材料力学性能试验与数值模拟如图4所示,反求所得材料力学性能参数如表1所示。通过力学性能试验与数值分析曲线(如图2所示)对比可以看出,CFRP在准静态拉伸断裂前,应力应变曲线趋近于线性变化,材料表现为线弹性性质,无明显的屈服特征。同时,由准静态单向拉伸应力应变曲线可以明显看出CFRP断裂失效表现为明显的脆性断裂特征。

CFRP汽车顶盖数值模型
▲▲▲
采用ABAQUS软件对汽车顶盖进行雪压分析时,取车身上半部作为研究对象,网格基本尺寸为5mm×5mm,四边形单元和三角形单元类型分别为S4R和S3,CFRP制件与钢制件之间采用胶粘模拟,胶粘单元类型选为COH3D8,对车身侧围截断位置约束X,Y,Z3个方向的平动,评判顶盖在重力载荷、1.28kPa的雪压工况及卸掉雪压载荷3种工况条件下CFRP汽车顶盖是否会发生屈曲现象,雪压分析有限元模型如图5所示。加载过程中,根据汽车顶盖在室外积雪过程的实际情况,将一个复杂的非线性动载问题简化为分布均匀加载的静态刚强度试验问题。同时,将乘用车顶盖积雪这一随机过程量化,通过分析加载前后顶盖位移变化来评判顶盖在积雪过程中是否出现永久变形和屈曲现象,以此来评判优化结果的可行性。数值分析采用隐式静态几何非线性算法,考虑了几何非线性、边界条件非线性和卸载后的残余变形,对CFRP汽车顶盖进行雪压屈曲分析,了解CFRP汽车顶盖的承载与变形能力,判断是否满足汽车顶盖刚度要求。

CFRP汽车顶盖铺层优化设计
1、初始模型雪压分析
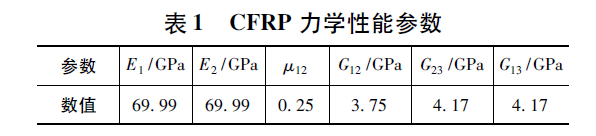
考虑到CFRP性能和汽车顶盖轻量化要求,在初步设计阶段采用4层CC-P400-12作为环氧树脂LTC-6010A/B的增强材料,厚度约为1.0mm,并通过数值分析来校核顶盖刚度是否满足相关要求,模拟积雪压力时顶盖位移变化简图和最大变形位置的压力-位移曲线,如图6所示,其中,数值模型在施加压力时载荷采取线性增加方式。由图6(a)~图6(c)位移变化云图可知,4层CFRP汽车顶盖位移随着压力的增加而增大,且初始最大变形位置发生在CFRP汽车顶盖后横梁与后支撑梁之间的A点;随后载荷继续增加,最大变形位置由A点转移到B点。由图6(d)可见,在4层CFRP汽车顶盖受压初始阶段(阶段Ⅰ)具有较好的抗变形能力;当压力达到1.12kPa时(阶段Ⅱ),4层CFRP汽车顶盖位移由1.27mm激增至18.63mm,这表明4层CFRP汽车顶盖出现几何软化响应,发生屈曲现象;而后当压力达到1.18kPa后(阶段Ⅲ),4层CFRP汽车顶盖刚度继续增加,最大变形达到24.17mm。由于4层CFRP汽车顶盖在受压过程中出现屈曲现象,故无法满足雪压刚度要求。

2、 CFRP汽车顶盖铺层优化设计
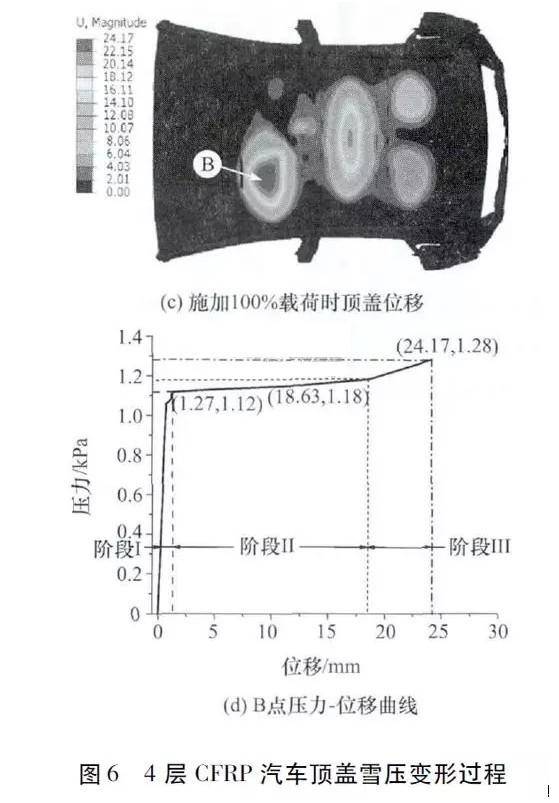
由4层CFRP汽车顶盖刚度计算结果可知,在顶盖受载过程中该铺层方案无法满足相应的雪压分析要求,故在同时考虑制造工艺约束和顶盖雪压分析要求的条件下对CFRP汽车顶盖进行铺层优化设计。在优化设计过程中采用自由尺寸优化,尺寸优化和复合材料层组优化3种优化方法,优化流程如图7所示。
2.1 自由尺寸优化
在初始设计过程中,汽车CFRP顶盖刚度能较好地满足刚度要求,通过自由尺寸优化来获取每种铺层角度的最佳铺层厚度。在自由尺寸优化过程中为复合材料建立与铺层角度相对应的几个超级层,该阶段每一铺层角度所在超级层厚度可连续变化。优化时,对各纤维铺层角度的铺层厚度进行优化,优化约束为汽车CFRP顶盖任意节点位移,优化目标为汽车CFRP顶盖质量最小,优化数学表达式如下所示:
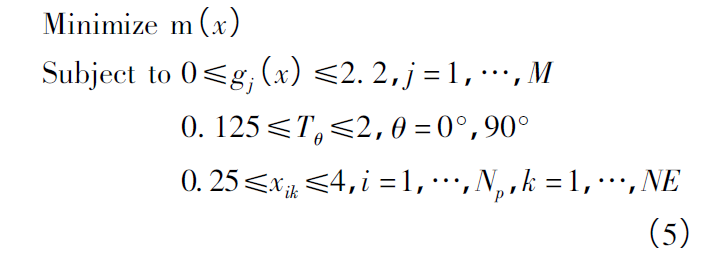
式中:m(x)为顶盖质量;gj(x)为第j个约束响应;M为总的约束数量;Tθ为对应铺层角度的铺层厚度;xik为第i个超级层中第k个单元的厚度;NE为单元数量;Np为超级层数量。
为使结构能较好地满足装配工艺和制造工艺要求,在优化设计过程中取制件总体厚度为制造约束目标:
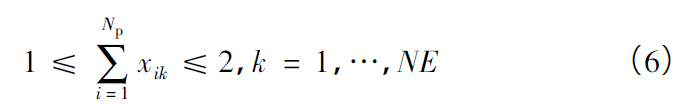
从而使得优化结果更好地满足实际要求。
2.2 尺寸优化
通过自由尺寸优化,能较好地确定每种铺层角度所需的铺层厚度,但由于层合板在制备过程中有一定的厚度要求,且铺层数量对制件的力学性能均有较大影响,所以研究中通过尺寸优化设计将制件单层厚度与设计变量之间的关系进行耦合分析,以获得每种铺层角度在给定铺层厚度条件下的最佳铺层数量。尺寸优化数学模型除采用与自由尺寸优化相同的模型外,还需建立多个设计变量之间的关系。尺寸优化设计过程中,一个设计变量与其他设计变量间的关系可表示为

在该优化过程中,同时兼顾了工艺制造过程中单层结构的制件厚度,在本次优化设计过程中设置每一铺层角度单层结构的厚度是相等的,即取t=0.25mm,在前期优化所得单种角度厚度基础上计算制件总的铺层层数:

式中:Ni为每种铺层角度对应的铺层层数;Ti为每个角度对应的总的铺层厚度。
在该优化设计过程中,对每一纤维铺层角度的厚度变量都进行了计算,并最终确定了每一纤维铺层角度所需的最佳铺层层数和CFRP汽车顶盖所需设计的总的厚度尺寸。
2.3 层组优化
CFRP的力学性能与纤维角度的排列顺序有着紧密的关系,在层组优化阶段,实际的目的是为了获得结构的最大刚度系数矩阵,从而使结构的刚度达到最大。在CFRP制备过程中,铺层结构设计应避免固化过程中由于弯曲、拉伸和扭转等耦合效应引起的翘曲变形和树脂裂纹,为此在铺层设计过程中应避免使用同一方向的铺层组,如果使用,应不多于4层。在层组优化设计阶段考虑了该制造工艺约束,因此本文中选取同一铺层角度连续铺层数量最多为两层,以使顶盖制造能较好地满足制造工艺要求。
经自由尺寸优化、尺寸优化和层组优化后得到CFRP顶盖铺层数量为6层,铺层顺序为[0/90/90/0/0/90],单层厚度为0.25mm,如图8所示,其中11101~11103及12101~12103分别代表各铺层组编号。

3、 优化结果与分析
经自由尺寸优化、尺寸优化和层组优化之后,对CFRP汽车顶盖再次进行雪压分析,分析结果表明,6层CFRP汽车顶盖在进行数值分析的过程中,顶盖最大变形量为1.922mm,与钢制顶盖分析结果0.769mm对比可见,虽然变形量大于钢制顶盖变形量,但变形依然处于弹性范围之内,未出现明显的屈曲现象,且在整个分析过程中,6层CFRP顶盖的位移变化趋势比4层CFRP顶盖稳定,因此判断6层CFRP顶盖未出现明显的屈曲现象,刚度能满足要求,最终顶盖位移云图和顶盖压力-位移变化曲线如图9和图10所示。
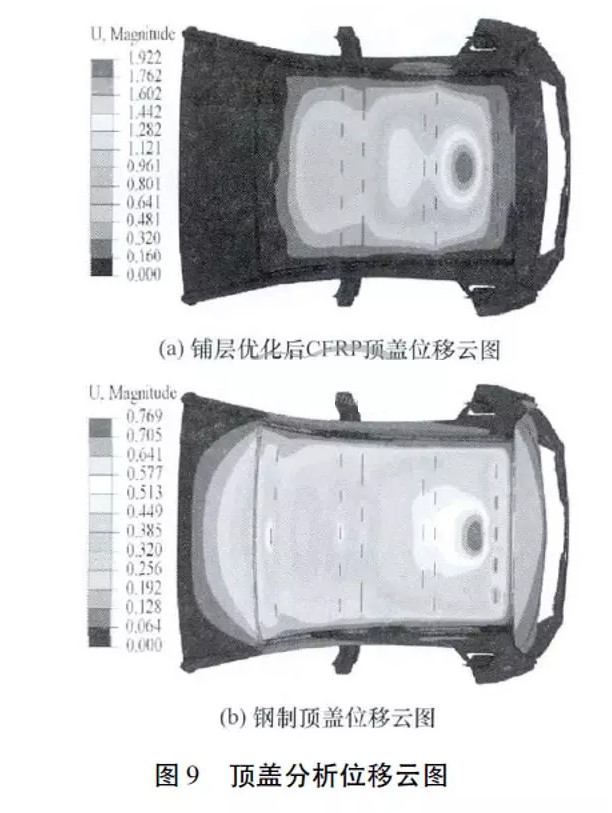
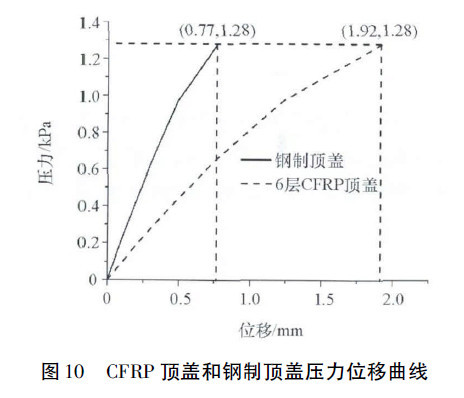
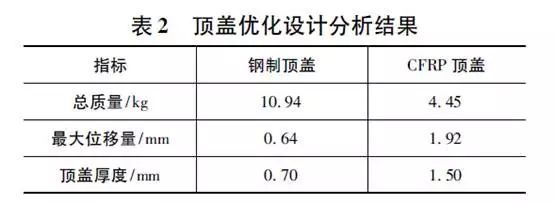
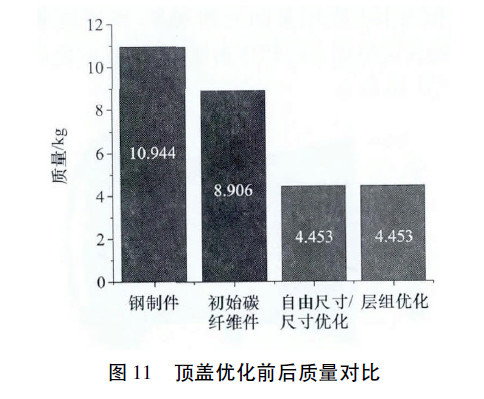
通过优化使CFRP顶盖在满足刚度及工艺制造等因素的条件下质量有了较大幅度的减小,结果如表2所示。钢制顶盖初始质量为10.944kg,汽车CFRP顶盖优化设计前的设计标准质量为8.906kg,优化后顶盖质量降低至4.453kg,较设计标准质量减轻了50%,与钢制件相比减轻了59.3%,如图11所示。
结 论
本文中围绕汽车CFRP顶盖铺层优化设计开展了材料制备、材料力学性能测定和数值模拟分析,并最终通过自由尺寸优化、尺寸优化和层组优化,完成了汽车CFRP顶盖铺层优化设计,得出以下结论。
(1)CFRP数值模拟曲线与力学性能试验曲线对比结果,误差在5%以内,验证了CFRP建模的有效性、选用材料本构模型参数和失效准则可用于后续的数值模拟。
(2)在优化过程中同时兼顾了制造工艺约束和制件刚度两方面的要求,较好地克服了仅使用理论算法控制制件刚度的局限性,使制件在满足刚度要求的同时,成型工艺可行性更好。
(3)将CFRP与传统的钢材对比发现,CFRP刚度和强度都较金属材料有较大的提升,尤其是在汽车结构轻量化方面的效果显著,通过优化,汽车CFRP顶盖质量比钢制顶盖减轻了59.3%。
来源:期刊—汽车工程
作者:肖志,杜庆勇,莫富灏等
(湖南大学,汽车车身先进设计制造国家重点实验室)
举报 0
收藏 0
分享 121
-
旭化成首战全球供应链管理大赛斩获佳绩
2025-03-03 -
旭化成授权斯尔邦高纯度碳酸盐生产技术,助力二
2024-12-13 -
华为尊界S800的座椅会有什么亮点?
2024-11-27 -
博世最新宣布裁员7000人
2024-11-06
编辑推荐
最新资讯
-
全球产业链聚沪 共探双碳新路径 SNEC
2025-04-18 18:05
-
柯马签订具有约束力的协议收购 Autom
2025-04-17 13:01
-
高效协同新范式:比亚迪叉车领创智能
2025-04-17 10:04
-
埃马克德国总部迎来中国社科院工业经
2025-04-15 09:40
-
埃马克这项全新应用即将在CIMT惊艳首
2025-04-15 09:37