汽车底盘零件高强钢内高压成形技术解析
大型汽车注塑件产品由于其结构复杂、尺寸较大,因而在实际生产中容易出现诸如体积收缩率大、翘曲变形大、熔接痕多等缺陷。这些缺陷会严重降低产品的质量合格率,在一定程度上增加了生产成本的投入。
近年来,注塑 CAE 技术在塑料产品开发和模具设计行业中占据着不可或缺的地位。汽车仪表板是汽车内饰件里的重要组成部分,王良柱等 通过Moldflflow 分析了汽车仪表板本体骨架的翘曲变形主要原因,根据塑件成型时的纤维取向规律改变塑件结构进而优化了塑件的翘曲变形,吴俊超 借助Moldflflow 软件和正交实验对汽车仪表板注塑模具进行了优化分析,李渊博等 利用 Moldflflow 软件对重卡仪表板本体注塑分别进行了料厚、翘曲变形和体积收缩率的分析,探究了塑件材料和塑件结构对塑件成型质量的影响。
目前国内外对汽车仪表板注塑数值模拟的研究还存在很多不足之处,笔者研究的汽车仪表板结构复杂,成型质量要求较高,故以翘曲变形和体积收缩率这两个目标来进行优化探究,采用了较为智能的 BP 神经网络和多目标遗传算法组合方式来进行汽车仪表注塑工艺参数的优化。
塑件结构及有限元模型
塑件三维模型
以某汽车仪表板为研究对象,采用 CATIA 建立汽车仪表板的三维零件模型,该仪表板的基本尺寸为 1 360.11 mm×559.11 mm×459.58 mm,平均壁厚为 2.41 mm,最大壁厚为 11.80 mm,如图 1 所示,该汽车仪表板塑件结构较复杂且尺寸较大,属于大型注塑件产品,注塑质量要求仪表板外观面无明显熔接痕、气穴等缺陷。

a—主视图;b—俯视图;c—左视图
图 1 汽车仪表板模型三视图
塑件有限元模型
将汽车仪表板三维模型导入 CAD doctor 中进行模型转换的预处理及修复以便于后续有限元模型的建立,利用 Moldflflow 对修复后的模型进行网格划分,网格划分结果如图 2 所示,网格划分质量见表 1。
图 2 汽车仪表板有限元模型
初步工艺模拟分析
笔者研究的汽车仪表板是硬塑仪表板,要求有一定的弹塑性和刚度以及高的尺寸稳定性和良好的力学性能,因此仪表板材料选择上海普利特复合材料制造的聚丙烯 / 三元乙丙橡胶 / 质量分数 20%。
表 1 网格划分质量
滑石粉 (PP+EPDM-T20),材料主要工艺性能见表 2。依据所选材料的工艺性能、塑件结构特点以及注塑经验,设定初步的工艺参数见表 3,数值模拟后得到的翘曲变形量为 9.556 mm,体积收缩率为10.72%,如图 3 所示。
表 2 材料的主要工艺性能
表 3 初步数值模拟得到的工艺参数组合
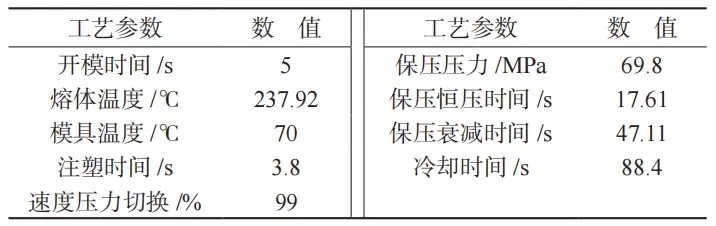
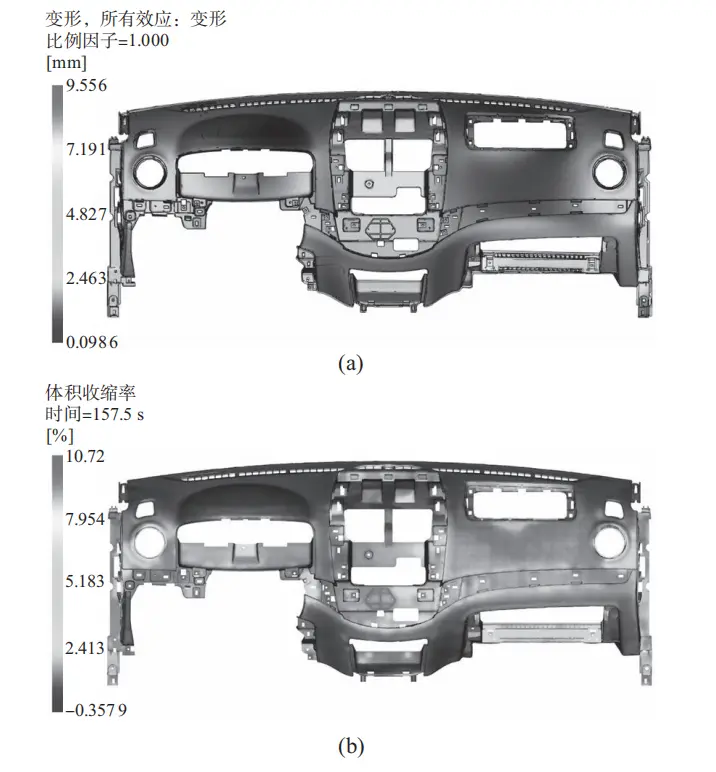
a—翘曲变形量;b—体积收缩率
图 3 初步数值模拟得到的翘曲变形量与体积收缩率
Box-Behnken 试验设计
在建立数据拟合模型前需要获取一定数量的试验数据,科学的试验设计方法能够获得良好全面的所研究对象的信息,笔者采用 Box-Behnken 试验设计进行试验数据的获取,其特点是所需的因素水平较少,设计点较少,并且能够高效地获得拟合模型的系数。
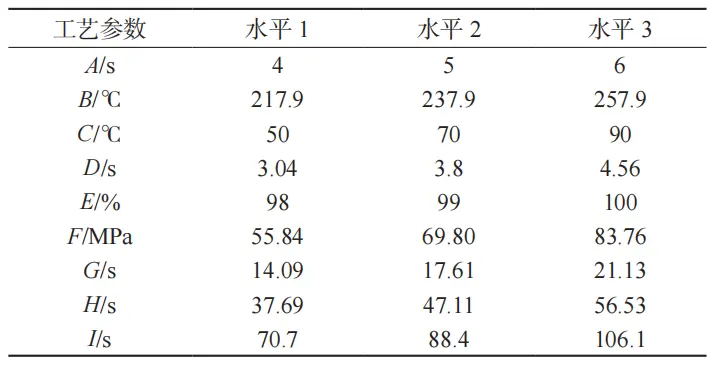
选取开模时间(A)、熔体温度(B)、模具温度(C)、注塑时间(D)、速度压力切换(E)、保压压力(F)、保压恒压时间(G)、保压衰减时间(H)、冷却时间(I)这9个工艺参数作为试验因子,以翘曲变形量(X)和体积收缩率(Y)为目标变量,进行9因子3水平Box-Behnken试验设计,工艺参数范围见表4。
表 4 工艺参数取值范围
根据 Box-Behnken 试验设计以及数值模拟过程得到了 130 组试验数据结果,考虑到文章篇幅的大小,只列出如表 5 所示的部分数据结果。
表 5 Box-Behnken 试验设计表部分数据

BP 神经网络模型的建立
人工神经网络是无需在了解输入和输出之间函数关系式的前提下,就能凭借自身不断的训练进而去学习输入和输出之间的映射规则的一种智能信息处理系统,BP 神经网络是一种以 BP 算法为核心算法的反向传播神经网络,梯度下降法是 BP神经网络用来实现预测值和实际值之间的均方差和误差最小化的主要方式。BP 神经网络包含隐藏层、输入层和输出层这 3个组成部分,通常 BP 神经网络的隐藏层为 1,实际上隐藏层节点数通常根据经验公式和实际试验来确定,经验公式如下:
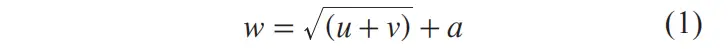
式 (1) 中 w,u,v 分别为隐藏层、输入层、输出层节点数,a 可以选择 1~10 之间的整数,笔者所建立的 BP 神经网络模型为 9 个输入节点,2 个输出节点,19 个隐藏层节点,神经网络模型拓扑图如图 4所示。
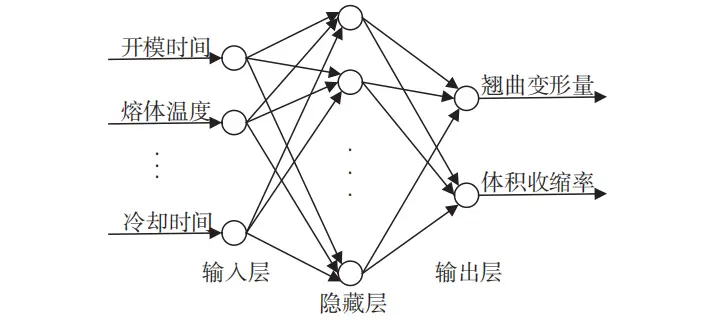
图 4 BP 神经网络模型拓扑图
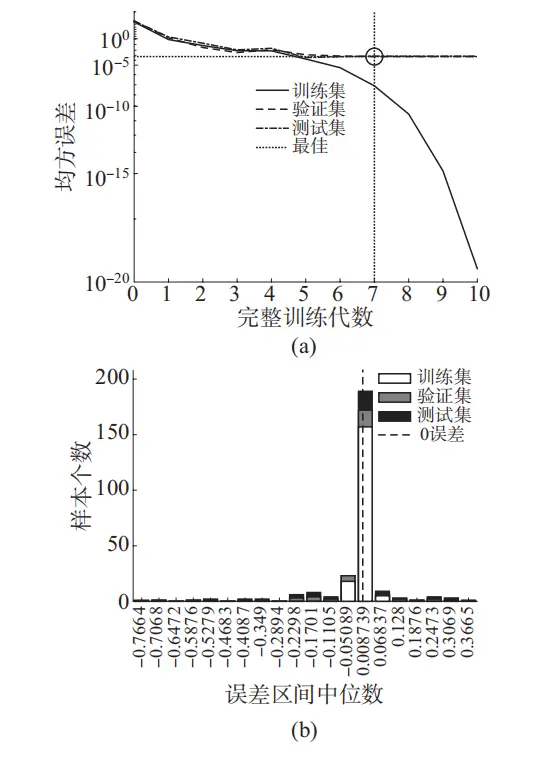
为了拟合较为精确的BP神经网络模型,从130组Box-Behnken试验中随机选取90组作为训练集数据,从剩下的40组试验数据里随机选取20组作为测试集数据,最后剩余的20组数据作为验证集数据,最大迭代数为1000,目标误差为1.00×10-7,学习率为0.01,最后得到的模型均方误差变化以及误差直方图如图5a、图5b所示,各数据集的回归性如图6所示。
从图 5a 中可以得到当数据集对模型完整训练
a—均方差变化图;b—误差直方图
图 5 均方差和直方图
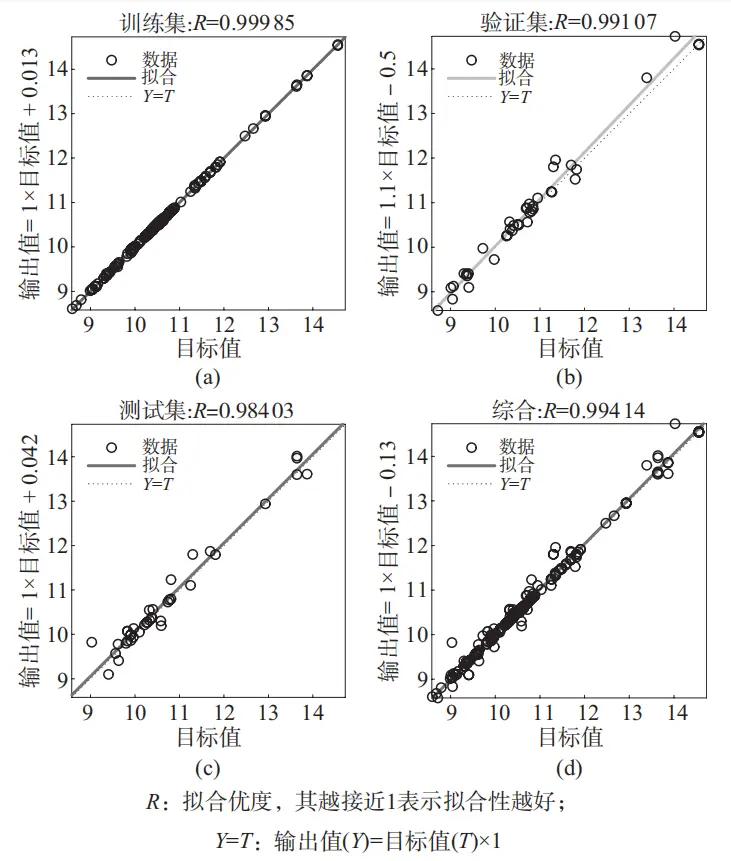
a—训练集;b—验证集;c—测试集;d—综合
图 6 模型回归能力图
7次时,验证集和测试集达到最小均方误差,图 5b中神经网络的输出值与样本原目标值的误差集中在0.008 739 左右,误差较小,图 6 中训练集、测试集、验证集的 R 均大于 0.9,表明了该拟合模型的线性化程度较高,结果良好。
基于多目标遗传算法的参数优化
非支配排序遗传算法 (NSGA-Ⅱ) 相较于传统多标遗传算法,计算复杂度降低了许多,其拥挤度和拥挤度比较算子的计算,改善了传统多目标遗传算法需要指定共享半径的适应度共享策略,为后续的快速排序提供了择优的标准,同时它可使解集域中解的个体均匀分布,保证了种群多样性。NSGA-Ⅱ的原理图如图 7 所示。
本文优化的多目标为汽车仪表板体积收缩率最小和翘曲变形量最小,Pareto 最优解集是多目标遗传算法求解结果中由多个目标均达到最优解的集合组成的解集,利用 NSGA-Ⅱ 进行优化求解,算法的种群个体总数为 200、交叉和变异概率分别为 0.8和 0.02、迭代次数为 200,优化得到体积收缩率和翘曲变形量 Pareto 最优解集如图 8 所示。
由于最优解集里存在多个解,为了使两个目标均达到最小化即两个目标权重均为 1,由此综合考虑优选出一个最佳组合方案为:翘曲变形量
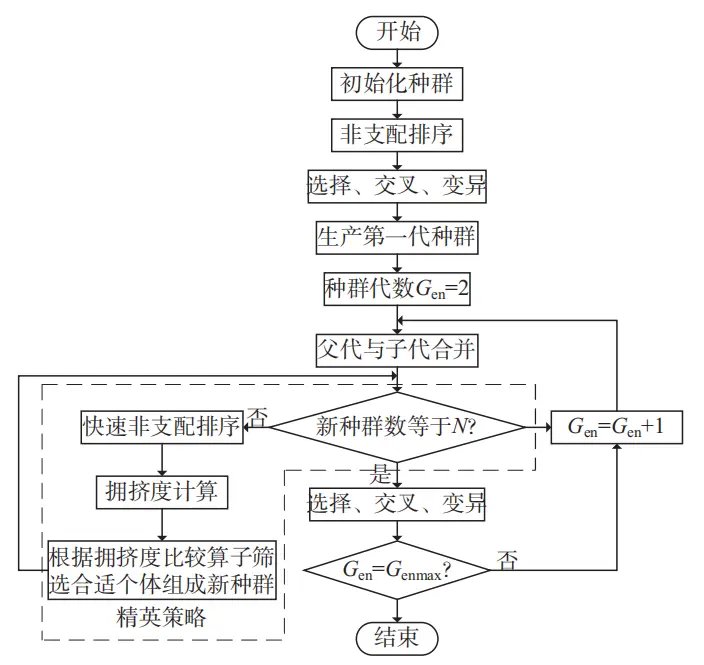
图 7 NSGA-Ⅱ 原理流程图
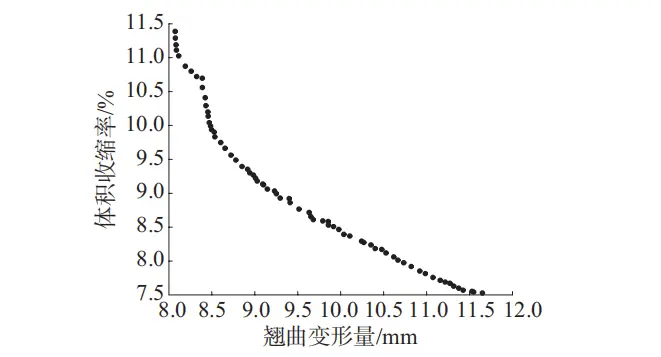
图 8 Pareto 最优解集
8.603 mm,体积收缩率 9.75%。此时的工艺参数为:开模时间 5.984 s,熔体温度 250.73℃,模具温度64.035℃,注塑时间 3.234 s,速度压力切换98.34%,保压压力 83.491 MPa,保压恒压时间 15.31 s,保压衰减时间 44.30 s,冷却时间 78.161 s。
数值模拟验证
为 了验证优化方法的准确性与可行性,在Moldflflow软件中设置好优化过的工艺参数进行模拟仿真,最后得到的结果如图9所示。图9中,仿真得到翘曲变形量为8.712mm,体积收缩率为9.8%,对比寻优得到的最优解,翘曲变形量误差为1.27%,体积收缩率误差为0.51%,误差均满足在3%以内,表明了所用优化方法的准确性。初步工艺模拟分析时的翘曲变形量为9.556mm,体积收缩率为10.72%,经过优化后的翘曲变形量减小了8.83%,体积收缩率降低了8.58%,塑件产品的质量得到了更进一步的提升,同时表明了所用优化方法的准确性与可行性。

a—翘曲变形量;b—体积收缩率
图 9 仿真验证结果
结论
(1) 以汽车仪表板体积收缩率和翘曲变形量作为优化目标,以开模时间、模具温度等9个工艺参数为影响因子,设计了Box-Behnken试验来获取不同水平影响因子所产生的目标结果数据,建立了BP神经网络模型,结合NSGA-Ⅱ最终确定了最优的注塑工艺参数为:开模时间5.984s,熔体温度250.73℃,模具温度64.035℃,注塑时间3.234s,速度压力切换98.34%,保压压力83.491MPa,保压恒压时间15.31s,保压衰减时间44.30s,冷却时间78.161s。
(2) 通过 Moldflflow 仿真验证发现仿真结果与寻优得到的结果之间误差较小,翘曲变形量优化了8.83%,体积收缩率优化了 8.58%。
-
冲压技术在电机叠片制造的应用
2024-09-06 -
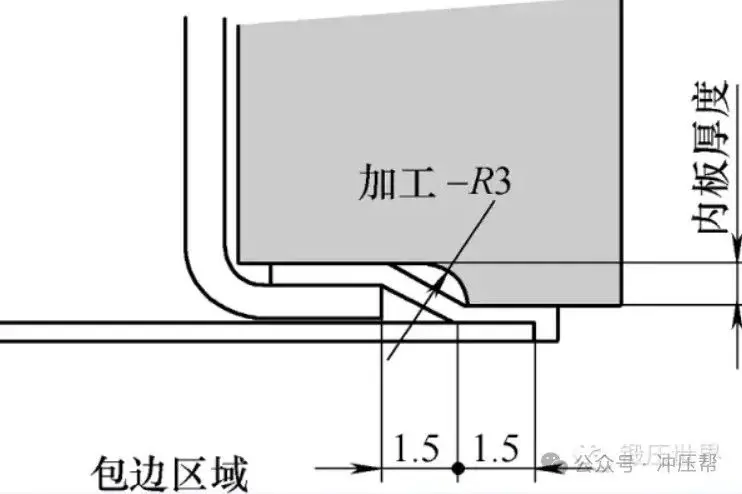
车身零部件包边质量控制要点
2024-09-05 -
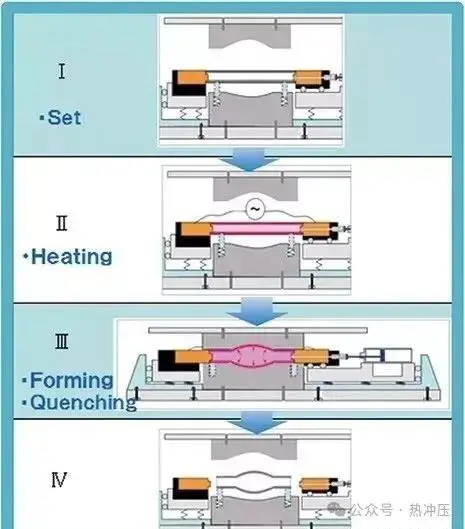
轻量化技术——热汽胀形工艺技术解析
2024-09-04 -
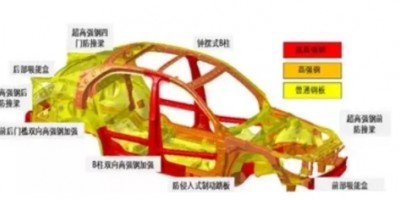
高强板车身件冲压技术
2024-09-02
最新资讯
-
[转载] 机床巨头埃马克:百年跌宕再
2025-03-31 12:42
-
从4S店到修理厂:FLIR ONE Pro USB-C
2025-03-28 16:05
-
比亚迪发布2024年ESG报告 以技术创新
2025-03-26 16:44
-
电装中国:以“技术+生态”双引擎驱
2025-03-24 19:07
-
杜尔中国海外项目-Stellantis 集团摩
2025-03-20 11:59