探求环形研抛工具最优加工位姿

机器人在研抛加工过程中需要确定研抛工具的位置及姿态，主控计算机根据研抛位姿求解机器人各个关节的相关状态量，并以机器人指令文件形式发送给机器人，从而控制机器人远程作业。机器人在研抛加工过程中的位姿需要根据工件表面外形来确定，在计算出研抛工具到达指定加工位置的位姿量后，由主控计算机将位姿量转化为机器人的关节运动量，然后使研抛工具到达指定加工位置。工件与机器人相关状态量的求解是在各自的坐标系下进行的，工件采用的坐标系是对工件进行建模、加工的坐标系，机器人采用的坐标系是机器人安装、工作的机器人基坐标系，二者相互独立。利用机器人对工件进行加工，需要将两坐标系建立关联来进行相关计算，坐标变换正是联系二者的桥梁。

本文对提出的位姿计算方法进行分析计算，并将算法在两种工件进行仿真验证，位姿计算方法是建立在MATLAB最优解工具基础上的一种计算方法，计算过程中采用了简化方程和缩小求解范围等方法使运算量大大减小，最终得到最优位姿，并在选定的工件上对计算的结果进行实验研究。该加工方法对于提高轿车的车身表面质量以及减轻工人手工打磨工作强度、提高生产线速度具有现实意义。

研抛工具到工件坐标系的转换

1.环形工具建模

以圆环面作为有效工作表面的工具，都可称为圆环面工具，形状如图1所示。圆环面角θ的全部360°都可作为工具的加工表面。但受结构限制，圆环面加工角会被工具体和机床主轴占去约90°，所以工具的θ角最大约可用到270°，这已能满足各种加工方式的需要。圆环面工具具有包络面的曲率分布可大幅度变化、便于建立模型精确计算、良好的加工性能以及良好的工艺性等特点，反圆环面工具和带圆角的平底工具都属于圆环面工具。

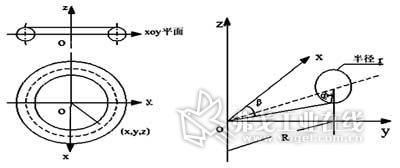
图1  环面工具基本参数

本文采用的是圆环体的研抛工具头，首先建立圆环体的参数方程：

公式1

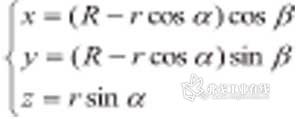
2.研抛工具坐标系到工件坐标系下的转换

确定研抛工具的位姿就是确定研抛工具坐标系在机器人基坐标系下的位姿矩阵。为了将研抛工具和被加工工件之间建立联系，首先要确定研抛工具坐标系在工件坐标系中的姿态矩阵。

经过计算分别绕X轴和Y轴旋转以及平移（a，b，c）后的变换矩阵如式2所示。

公式2

研抛工具位姿的计算方法和仿真

环形研抛工具经过两次转动和平动后到达加工位置，此时研抛工具与工件的接触点即是工件表面参数方程与环形研抛工具的参数方程联立后方程的解，再用求出的方程解在MATLAB中仿真位姿状态验证解的正确性。

1.球面工件的计算与仿真

为了将环形研抛工具表面点和球面工件表面点之间建立联系，建立如下方程组：

公式3

在MATLAB中解方程组，由于是三个方程解五个未知数的问题，引用MATLAB中最优解的工具，通过简化模型和约束条件，选取工具上的α=π/2，β=0点和工件上的θ'=π/4，φ'=π/4，点作为研究对象，选取适当的取值范围和初值，求得结果如图2所示。

图2   球面工件计算结果

即θ=0.7226弧度，φ=0.6597弧度，a=122.2135mm，b=-105.2446mm，c=120.0812mm，研抛工具加工球面工件的位姿仿真图如图3所示。

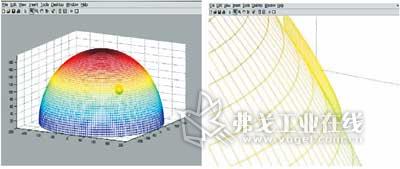
图3   研抛工具加工球面工件的位姿仿真图

2.椭球面工件的计算与仿真

为了将环形研抛工具表面点和椭球面工件表面点之间建立联系，建立如下的方程组：

公式4

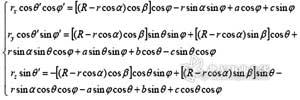
选取工具上的点α=π/2，β=0和工件上的θ'=π/4，φ'=π/4点作为研究对象，选取适当的取值范围和初值，求得结果如图4所示。

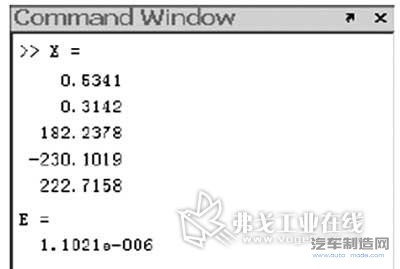
图4  椭球面工件计算结果

即θ=0.7226弧度，φ=0.6597弧度，a=122.2135mm，b=-105.2446mm，c=120.0812mm，研抛工具加工球面工件的位姿仿真如图5所示。

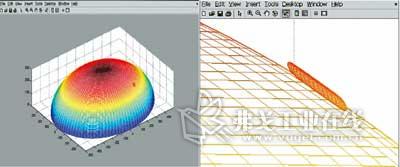
图5   研抛工具加工椭球面工件的位姿仿真

研抛工具位姿计算方法实验研究

1.工件的测量及曲线拟合

工件外形参数采用三坐标测量机测量。由于工件本身是回转体，只需测量工件外表面的一条母线，并对工件母线数据进行曲线的多项式拟合。经验证明选用三次多项式来进行曲线拟合的效果最好，得到的结果如图6所示，红色曲线即为拟合结果。

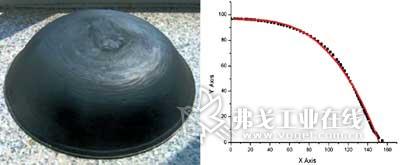
图6   工件实物及母线拟合

使用MATLAB 曲线拟合工具箱得到三次多项式拟合结果：

Linear model Poly3:

f(x) = p1*x^3 + p2*x^2 + p3*x + p4

Coefficients (with 95% confidence bounds):

p1 =-4.761e-005 (-5.38e-005, -4.141e-005)

p2 = 0.003877 (0.002488, 0.005266)

p3 = -0.1693(-0.2554, -0.08321)

p4 = 97.57(96.15, 98.98)

Goodness of fit:

SSE: 7.109，R-square: 0.9995

Adjusted R-square: 0.9993，RMSE: 0.7697

MATLAB 曲线拟合工具箱给出的图形显示结果如图7所示。图7不仅给出了曲线的多项式拟合结果，同时还把各个拟合数据点与实际数据点加以比较，从中可以很明显地看出采用三次多项式来对工件母线数据进行曲线拟合所得到的结果还是很令人满意的。

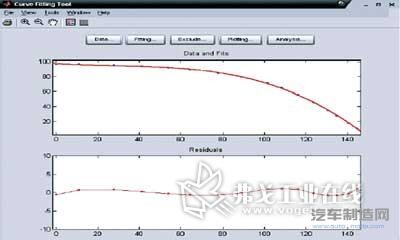
图7   拟合结果与数据偏差

2.工件模型的建立

通过采用多项式拟合的方法得到了工件母线的数学表达式（5），下一步进行工件建模。由于本实验工件是回转体，对于工件外表面的建模，可以通过母线的旋转实现。据式（5）利用三维工程软件Pro/ENGINEER 的参数化建模功能对工件进行实体建模，工件模型如图8所示，白色曲线为工件的母线。

图8   虚拟工件模型

公式5

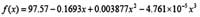
3.研抛工具位姿实验

生成工件模型之后，对工件模型进行数控仿真加工。数控仿真加工中的加工路径以及随后生成的数控加工代码即为应用在实际研抛加工中的加工路径和加工代码。利用MasterCAM 软件对虚拟工件模型进行数控加工之前，需要导入虚拟工件的三维实体模型。首先将虚拟工件模型以IGES 标准格式进行存储，然后在MasterCAM 软件中读取相应的IGES 文件，读取工件模型后的结果如图9所示。

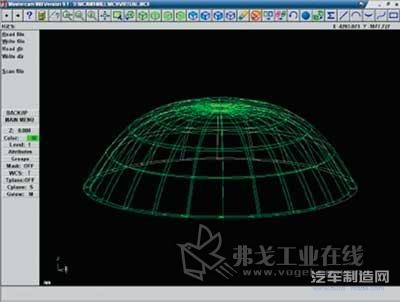
图9  导入虚拟工件模型

导入工作完成后，就可以根据工件模型上的已知点代入到方程组中去求得三个平动量和两个转动量，然后代入逆解公式6，求出机器人各关节变量的值，最终使研抛工具到达加工位置。

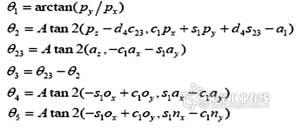
假设由机器人终端坐标系相对于机器人基坐标系的转换矩阵公式6，工具坐标系相对于机器人基坐标系的转换矩阵为数字，工具坐标系相对于机器人终端坐标系的转换矩阵为数字，工件上已知点坐标系相对于工件坐标系的转换矩阵为数字，工件坐标系相对于机器人基坐标系的转换矩阵为数字，从前文已知工具坐标系相对于工件坐标系的转换矩阵数字，则由工具坐标相对于机器人基坐标可用两种变换矩阵来表示：

公式7

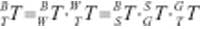
转换可得：

公式8

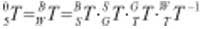
为了简化模型，我们选取机器人、机器人终端、工具及工件的坐标系相互平行，所以上式可表达为：其中l、m、n为机器人与工件坐标的平移量，nz为工具与机器人终端的Z向平移量，ax、ay、az为工件在工件坐标系下的坐标，经测量知l=m=0，n=1030mm，nz=110mm，取工件上点（0，80，84.2364），代入式（3）得到θ=0.4876弧度，φ= 0 弧度，a=51.2382mm，b=-102.2586mm，c=-115.3561mm，将已知和求得的数代入式（9），比较等号左右矩阵，再代入式（6）即可得到机器人各关节变量的值θ1=0，θ2=-0.1758，θ23=0.1053，θ3=-0.2811，θ4=0.8656，θ5=0（单位弧度）。图10为机器人到达计算位姿对工件进行加工。

图10   研抛工具到达工件加工点位姿

对于本文提出的研抛工具位姿计算方法，实验证明了机器人能够使研抛工具到达已知的工件位置点，从而验证了研抛工具位姿计算方法在机器人柔顺研抛自由曲面类工件中的可行性。

结束语

本文进行了机器人柔顺研抛自由曲面工件的位姿计算方法的推导及实验，研究了工件测量的方法、工件母线的多项式拟合、工件建模的方法、计算机与机器人的通信以及机器人实验的加工过程，详细阐述了计算的整个流程，最后对实验结果进行了分析，仿真结果表明计算方法是正确的（误差e-6mm→0 可以忽略），实验证明机器人能够使研抛工具按照计算结果到达已知的工件位置点，从而验证了本文提出的研抛工具位姿计算方法在机器人柔顺研抛车身类自由曲面工件中的可行性。